An introduction to DEM
The DEM was orginally developed in 1979 by Cundall and Stack to study behaviour of granular and particulate systems. It is a numerical method which models the movement and contact between each particle. [6]
Discrete element method is a numerical model capable of describing complicated behaviour of materials by using discretization scheme. Some of the DEM codes, like PFC3D (ITASCA, 2003) and EDEM (DEM Solutions, 2005) discretize material using a multiple-sphere method where the shape of a non-spherical particle is represented as an assembly of rigidly linked spheres. Once stress is applied to the assembly of spheres, elements interact with each other and these interactions are monitored contact by contact. The contact forces and displacements of an assembly are simply found by calculating the movements of individual particles. [7]
Key Features
The motion of an assembly is modeled particle by particle. There are three major steps in the analysis:
- internal force evaluation: calculation of contact forces;
- integration of equations of motion: calculation of elements displacemets;
- contact detection: in this step broken contacts are removed and new contacts are identified. [8]
In order to model the behaviour of each particle, these calculations are repeated for each time step. It is highly important to choose a proper time step for modelling. Time step should be so small that during a single time step disturbances from any sphere cannot propagate further than to its nearest neighbour. Only in this case, the resultant forces acting on sphere are determided by its iteraction with the elements with which it is in contact.
Two Main Assumptions
The interaction of elements is established by application of Newton's second law to spheres and force-displacement law at contacts.
Newton's second law:
F = ma
where F-resultant force, m-mass, a-acceleration, gives the acceleration of a particle resulting from the foces acting on it. The result acceleration is used to establish velocity and displacements.
Force-displacement law:
Fn = KnΔun
Fs = KsΔus
where Fn, Fs are the normal and tangential contact forces, Kn, Ks the normal and tangential stiffness at contact, Δun is the relative particle normal displacement, and Δus the incremental particle tangential displacement, see Figure 2 below. This law is used to find contact forces from known displacements.
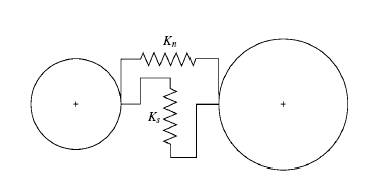
Figure 2 - Elastic interaction, normal and shear springs
(Kn, Ks respectively). [4]
In the case of an assembly of many spheres, the force-displacement law is applied at each contact of any sphere and the vectorial sum of these contact forces (Fn, Fs) is determined to generate the resultant force acting on that sphere (F). When these calculations are applied to every sphere, new accelerations (a) are established using Newton's second law. This procedure is repeated in a loop. [8]
DEM to Study Concrete Behaviour
Discrete Element Model was first introduced as a powerful tool in the analysis of discrete structures, modelling the behaviour of granular and particulate systems. However, with several enhancements proposed by several investigators, it is now possible to apply it in the analysis of continuum problems (e.g. Solids), especially those that are characterized by transformation from a continuum to a discontinuum. Such problems include failure of concrete structures, fragmentation of rock due to blasting and fracture of ceramics.

Figure 3 - View on cylindrical DEM specimen of Concrete. [4]
Donze and Hentz [9,10] have extended the DEM by introducing an interaction range, which allows study interactions between two spheres which are bonded together. This approach allows to simulate the behaviour of concrete and rocks.
A modified Mohr-Coulomb rupture criterion is used in the modelling of concrete behaviour, Figure 4. It is assumed that particles forming a body of concrete can sustain higher forces than those of normal contact interaction. The bond can be broken when a tensile force exceeds a maximum tensile force Fnmin. Once the bond is broken, new interactions are identified, which are not cohesive anymore. They are contact interactions which cannot undergo any tension force. Then a classical Coulomb criterion is used with a contact friction angle Φc. [9]

Figure 4 - Rupture criterion used in the DEM. [4]
» Next: EDEM