Analytical solution for elastic normal impacts
In order to understand the behaviour of particles and there interaction with each other as well as the relationship of applied forces on the particles. These are the numerical calculations for the elastic impact of two identical spheres with no spin along the line. Both spheres have the same material properties. This will help us to understand the behaviour of particles. [20]
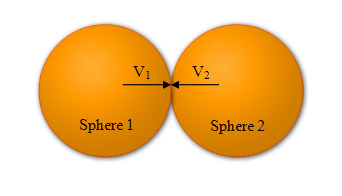
Figure 5, showing two identical spheres colliding into each other.
Where V1 and V2 donates to the incoming velocities of sphere 1 and sphere 2 respectfully, and the duration tduration of the collision of two identical spheres is given by the following equation:
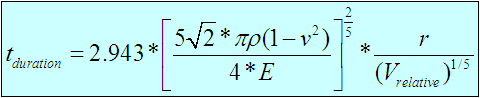
Where:
- E = the Young's modulus of the spheres materials
- ν = the Poisson's ratio
- ρ = the density of the spheres materials
- r = the radius of each sphere
Thus, the maximum normal contact displacement αmax for the elastic impact of two identical spheres with no spin along the line will be:
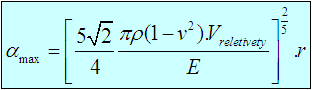
And the contact force PMax for the elastic impact of two identical spheres with no spin along the line.
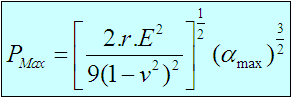
Analysis solution for a sphere impacting
on a rigid plane surface
In this experiment we are trying to analysis and investigate the impact of a solid sphere failing under gravity, into a rigid plane surface using the theory behinds Newton's second law of motion. [20]
The sphere has the same material properties as the rigid surface. Also the sphere's incoming velocity will be donated as V1. Also this experiment has been simulated using the EDEM software (see Simulation tape).
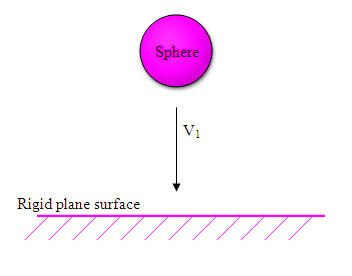
Figure 6, showing solid sphere colliding on a rigid surface.
The contact duration tduration for a sphere impacting on a rigid plane with incoming velocity V1 can be determined from the following equation:
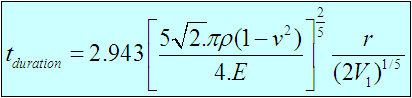
The maximum contact displacement αMax for a sphere impacting on a rigid plane with incoming velocity V1 can be determined using the following equation:
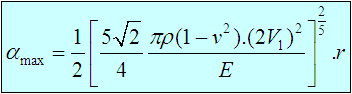
The maximum contact force PMax for a sphere impacting on a rigid plane with incoming velocity V1 can be determined from the following equation:
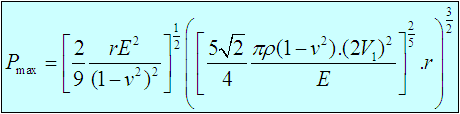
» Next: Simulation